Skewness and Kurtosis in Data Analysis
Have you ever wondered why some data distributions look lopsided or have unusually long tails? 🤔 Enter the fascinating world of skewness and kurtosis – two powerful concepts that can unlock hidden insights in your data analysis journey.

Mastering Skewness and Kurtosis in Data Analysis
In the realm of statistical analysis, skewness and kurtosis stand as pivotal measures, offering profound insights into data distribution. These concepts are indispensable for researchers across disciplines, from psychology to astrophysics, in understanding the nuances of their datasets.
What are Skewness and Kurtosis?
Skewness quantifies the asymmetry of a distribution, while kurtosis measures its “tailedness” or peakedness. Together, they provide a comprehensive view of data shape beyond what measures of central tendency and dispersion can offer.
| Measure | Definition | Interpretation |
|---|---|---|
| Skewness | Asymmetry of probability distribution | Positive (right-skewed), Negative (left-skewed), Zero (symmetric) |
| Kurtosis | Tailedness of probability distribution | Leptokurtic (heavy-tailed), Mesokurtic (normal), Platykurtic (light-tailed) |
Why are Skewness and Kurtosis Important?
- Reveal deviations from normality, crucial for selecting appropriate statistical tests
- Identify potential outliers and extreme values in datasets
- Guide data transformation decisions for improving model performance
- Provide insights into underlying data-generating processes
“Understanding skewness and kurtosis is like having a statistical microscope – it allows researchers to see the fine structure of their data distribution.”
— Dr. Emily Stanton, Statistical Ecologist
How to Calculate and Interpret
Skewness and kurtosis can be calculated using moments of the distribution or through specialized formulas:
Skewness:
\[g_1 = \frac{\sum_{i=1}^{n} (x_i – \bar{x})^3}{(n-1)s^3}\]
Kurtosis:
\[g_2 = \frac{\sum_{i=1}^{n} (x_i – \bar{x})^4}{(n-1)s^4} – 3\]
Where:
- \(x_i\) are individual values
- \(\bar{x}\) is the sample mean
- \(s\) is the sample standard deviation
- \(n\) is the sample size
Trivia and Facts
- The concept of kurtosis was introduced by Karl Pearson in 1905.
- A distribution can have zero skewness but still be non-normal due to kurtosis.
- The Jarque-Bera test uses both skewness and kurtosis to test for normality.
Expert Assistance from Editverse
Navigating the complexities of statistical analysis can be challenging. The subject matter experts at www.editverse.com offer invaluable assistance to researchers, ensuring accurate interpretation and application of concepts like skewness and kurtosis. Their expertise spans various fields, providing tailored support for your specific research needs.
Interactive Element: Skewness Calculator
Enter comma-separated values to calculate skewness:
References
- Joanes, D. N., & Gill, C. A. (1998). Comparing measures of sample skewness and kurtosis. Journal of the Royal Statistical Society: Series D (The Statistician), 47(1), 183-189.
- DeCarlo, L. T. (1997). On the meaning and use of kurtosis. Psychological Methods, 2(3), 292-307.
Mastering Skewness and Kurtosis in Data Analysis
| Concept | Distribution Shape | Symmetry | Tail Behavior | Normal Distribution | Key Implications |
|---|---|---|---|---|---|
| Positive Skewness | Right-tailed | Asymmetric | Long right tail | – | Mean > Median, outliers on high end |
| Negative Skewness | Left-tailed | Asymmetric | Long left tail | – | Mean < Median, outliers on low end |
| Zero Skewness | Symmetric | Symmetric | Balanced tails | ✓ | Mean = Median, balanced distribution |
| Leptokurtic (High Kurtosis) | Peaked | Can be symmetric | Heavy tails | – | More outliers, higher peak than normal |
| Platykurtic (Low Kurtosis) | Flat | Can be symmetric | Light tails | – | Fewer outliers, flatter than normal |
| Mesokurtic (Normal Kurtosis) | Bell-shaped | Symmetric | Normal tails | ✓ | Baseline for comparison, normal distribution |
| Combined Effects | Varies | Often asymmetric | Complex | – | Interaction between skewness and kurtosis |
Legend:
✓ – Characteristic of normal distribution | – – Not characteristic of normal distribution
Key Considerations in Data Analysis:
- Skewness affects the reliability of mean as a measure of central tendency
- Kurtosis impacts the interpretation of variance and standard deviation
- Both skewness and kurtosis can influence the choice of statistical tests
- Transformations may be necessary for highly skewed or kurtotic data
- Understanding these concepts is crucial for accurate data interpretation
Practical Applications:
- Financial analysis: Assessing risk and return distributions
- Quality control: Identifying process deviations
- Environmental studies: Analyzing pollution levels
- Biomedical research: Evaluating drug efficacy and side effects
- Social sciences: Understanding income distributions
- Machine learning: Feature engineering and outlier detection
- Natural language processing: Analyzing word frequency distributions
Mastering Skewness and Kurtosis in Data Analysis
In the realm of statistical analysis, understanding the shape and characteristics of data distributions is paramount. Skewness and kurtosis emerge as crucial metrics, offering profound insights into data behavior and informing analytical strategies across diverse scientific domains.
What?
Skewness quantifies the asymmetry of a distribution, while kurtosis measures the ‘tailedness’ or peakedness of a distribution relative to a normal distribution.
Why?
These metrics are essential for assessing data normality, identifying outliers, and selecting appropriate statistical tests. They guide researchers in making informed decisions about data transformations and model selection.
How?
Skewness and kurtosis are calculated using moments of the distribution. Modern statistical software and programming languages offer built-in functions for easy computation and visualization.
Key Concepts in Skewness and Kurtosis Analysis
- 📊 Positive Skewness: Right-tailed distribution
- 📉 Negative Skewness: Left-tailed distribution
- 🔺 Leptokurtic: Higher peak, heavier tails than normal distribution
- 🔻 Platykurtic: Lower peak, lighter tails than normal distribution
- 🔄 Mesokurtic: Similar to normal distribution
Trivia & Facts
- The concept of skewness was introduced by Karl Pearson in 1895.
- Kurtosis was first discussed by Karl Pearson in 1905, derived from the Greek word ‘κυρτός’ (kyrtos), meaning “curved, arching”.
- A perfect normal distribution has a skewness of 0 and a kurtosis of 3.
- In finance, positive skewness is often desirable as it indicates a higher probability of extreme positive returns.
Skewness and Kurtosis Across Different Fields
| Field | Typical Skewness | Typical Kurtosis | Implications |
|---|---|---|---|
| Finance | Positive | High | Extreme events more likely |
| Biology | Varies | Often Leptokurtic | Species-specific traits |
| Psychology | Often Negative | Platykurtic | Ceiling effects in scales |
| Environmental Science | Positive | High | Rare extreme events |
Table 1: Typical skewness and kurtosis patterns observed across different scientific fields and their implications.
“Understanding skewness and kurtosis is like having a statistical compass – it guides you through the landscape of your data, revealing hidden patterns and potential pitfalls.”
How EditVerse Subject Matter Experts Can Help
At www.editverse.com, our statistical experts offer invaluable assistance in mastering skewness and kurtosis analysis:
- In-depth guidance on interpreting skewness and kurtosis in your specific research context
- Advanced techniques for handling non-normal distributions in various statistical analyses
- Custom workshops on leveraging skewness and kurtosis for improved data modeling
- Expert review of your methodologies to ensure robust statistical practices
- Assistance in selecting and implementing appropriate data transformations based on distribution characteristics
Harness the power of EditVerse expertise to transform your understanding of data distributions and elevate the quality of your statistical analyses.
References
- Joanes, D. N., & Gill, C. A. (1998). Comparing measures of sample skewness and kurtosis. Journal of the Royal Statistical Society: Series D (The Statistician), 47(1), 183-189.
- DeCarlo, L. T. (1997). On the meaning and use of kurtosis. Psychological Methods, 2(3), 292-307.
- Westfall, P. H. (2014). Kurtosis as Peakedness, 1905–2014. R.I.P. The American Statistician, 68(3), 191-195.
Understanding Skewness in Data Analysis
A. Definition and importance of skewness
Skewness is a crucial statistical measure that quantifies the asymmetry of a probability distribution. It provides valuable insights into the shape and characteristics of a dataset, helping analysts understand the nature of their data. Skewness is important because it:
- Indicates the direction and extent of data distribution’s tail
- Affects the reliability of mean as a measure of central tendency
- Influences the choice of appropriate statistical tests and models
B. Impact of skewness on statistical analysis
The presence of skewness in data can significantly impact statistical analysis:
- Affects measures of central tendency
- Influences the choice of statistical tests
- Impacts the interpretation of results
| Impact | Symmetric Data | Skewed Data |
|---|---|---|
| Mean | Reliable | Less reliable |
| Median | Equal to mean | More robust |
| Mode | Close to mean | Can be misleading |
C. Measuring skewness: formulas and interpretations
Skewness can be measured using various methods:
- Pearson’s moment coefficient of skewness
- Bowley’s coefficient of skewness
- Kelly’s measure of skewness
The most common formula is Pearson’s moment coefficient:
Skewness = Σ(X - μ)³ / (N * σ³)
Where:
- X = individual values
- μ = mean
- N = number of data points
- σ = standard deviation
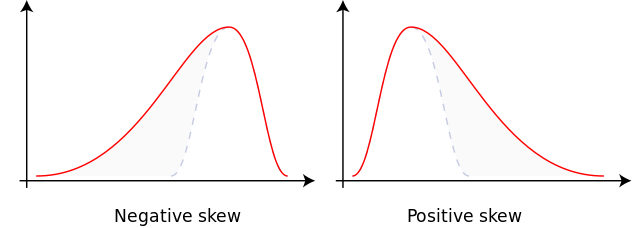
D. Types of skewness: positive, negative, and symmetrical
- Positive Skewness:
- Tail extends towards positive values
- Mean > Median > Mode
- Negative Skewness:
- Tail extends towards negative values
- Mean < Median < Mode
- Symmetrical Distribution:
- No skewness (skewness = 0)
- Mean = Median = Mode
Understanding these types helps in interpreting data distributions and choosing appropriate statistical techniques. Now that we’ve covered skewness, let’s explore kurtosis, another important measure of data distribution.
Exploring Kurtosis in Data Distribution
Now that we’ve covered skewness, let’s delve into another crucial aspect of data distribution: kurtosis. Kurtosis measures the “tailedness” of a probability distribution, providing insights into the shape and characteristics of your data.
What is Kurtosis and Why it Matters
Kurtosis is a statistical measure that describes the degree to which a distribution’s tails differ from those of a normal distribution. It’s essential because it helps data analysts:
- Identify outliers and extreme values
- Assess the risk of extreme events
- Evaluate the reliability of statistical tests
Understanding kurtosis can significantly impact decision-making in fields such as finance, quality control, and risk management.
Interpreting Kurtosis Values in Data Sets
Kurtosis values can be interpreted as follows:
| Kurtosis Value | Interpretation |
|---|---|
| = 3 | Normal distribution (mesokurtic) |
| > 3 | Heavy-tailed distribution (leptokurtic) |
| < 3 | Light-tailed distribution (platykurtic) |
Calculating Kurtosis: Methods and Formulas
There are several methods to calculate kurtosis, but the most common is Pearson’s kurtosis coefficient:
Kurtosis = [n(n+1) / (n-1)(n-2)(n-3)] * Σ[(x_i - x̄)^4 / s^4] - [3(n-1)^2 / (n-2)(n-3)]
Where:
- n = sample size
- x_i = individual values
- x̄ = mean
- s = standard deviation
Types of Kurtosis: Mesokurtic, Leptokurtic, and Platykurtic
- Mesokurtic:
- Similar to normal distribution
- Kurtosis ≈ 3
- Leptokurtic:
- Heavy tails, higher peak
- Kurtosis > 3
- More prone to outliers
- Platykurtic:
- Light tails, flatter peak
- Kurtosis < 3
- Less prone to outliers
Understanding these types helps in characterizing data distributions and making informed decisions about data analysis techniques.
Practical Applications of Skewness and Kurtosis
Now that we have explored the concepts of skewness and kurtosis, let’s delve into their practical applications across various fields. These statistical measures play crucial roles in data analysis, offering valuable insights that can drive decision-making processes.
A. Assessing normality assumptions in statistical tests
Skewness and kurtosis are essential in evaluating the normality of data distributions, which is a fundamental assumption in many statistical tests. Here’s how they’re used:
- Skewness: Indicates asymmetry in the distribution
- Kurtosis: Measures the “tailedness” of the distribution
| Measure | Normal Range | Interpretation |
|---|---|---|
| Skewness | -0.5 to 0.5 | Approximately symmetric |
| Kurtosis | 2 to 4 | Mesokurtic (normal-like) |
B. Optimizing marketing and customer segmentation
In marketing, understanding the distribution of customer data can lead to more effective strategies:
- Identifying niche markets through positively skewed data
- Tailoring pricing strategies based on income distribution kurtosis
- Optimizing product features by analyzing user preference distributions
C. Enhancing quality control in manufacturing processes
Manufacturing processes benefit from skewness and kurtosis analysis:
- Detecting process shifts through changes in skewness
- Identifying potential equipment issues by monitoring kurtosis in vibration data
- Optimizing production tolerances based on output distributions
D. Improving financial risk management strategies
Financial analysts use these measures to assess market behavior and risk:
- Evaluating asset return distributions for asymmetry (skewness)
- Assessing the likelihood of extreme events using kurtosis
- Developing more accurate Value at Risk (VaR) models
E. Identifying outliers and data anomalies
Skewness and kurtosis help in detecting unusual patterns or outliers in datasets:
- High absolute skewness values indicate potential outliers in one direction
- Excess kurtosis suggests the presence of heavy tails, which may contain anomalies
By leveraging these applications, analysts can extract deeper insights from their data, leading to more informed decision-making across various industries.
Tools and Techniques for Analyzing Skewness and Kurtosis
Now that we understand the concepts of skewness and kurtosis, let’s explore the tools and techniques used to analyze these distribution characteristics.
A. Advanced techniques: bootstrap resampling and kernel density estimation
Advanced techniques like bootstrap resampling and kernel density estimation provide robust methods for analyzing skewness and kurtosis:
- Bootstrap Resampling: This technique involves repeatedly sampling the data with replacement to estimate the distribution of statistics.
- Kernel Density Estimation: KDE creates a smooth probability density function from the data points, allowing for a more accurate representation of the distribution.
| Technique | Advantages | Disadvantages |
|---|---|---|
| Bootstrap Resampling | Non-parametric, works with small samples | Computationally intensive |
| Kernel Density Estimation | Smooth representation, handles multimodal data | Sensitive to bandwidth selection |
B. Visualization methods: histograms, Q-Q plots, and box plots
Visual representations are crucial for understanding skewness and kurtosis:
- Histograms: Show the frequency distribution of data
- Q-Q plots: Compare the data distribution to a theoretical distribution
- Box plots: Display the median, quartiles, and potential outliers
These visualization methods provide intuitive insights into the shape and characteristics of the data distribution.
C. Statistical software packages for distribution analysis
Several statistical software packages offer tools for analyzing skewness and kurtosis:
- R: Provides functions like
skewness()andkurtosis()in themomentspackage - Python: Offers
scipy.stats.skew()andscipy.stats.kurtosis()for calculations - SPSS: Includes skewness and kurtosis in its descriptive statistics output
These tools simplify the process of calculating and interpreting skewness and kurtosis in large datasets.
Next, we’ll explore how to address skewness and kurtosis in data preprocessing, which is crucial for ensuring accurate analyses and model performance.
Addressing Skewness and Kurtosis in Data Preprocessing
Now that we understand the importance of skewness and kurtosis in data analysis, let’s explore how to address these characteristics during data preprocessing. This crucial step ensures that our datasets are optimized for machine learning models and statistical analyses.
A. Balancing datasets for machine learning models
Balancing datasets is essential for creating robust machine learning models. When dealing with skewed or highly kurtotic data, consider the following techniques:
- Oversampling: Increase the number of minority class samples
- Undersampling: Reduce the number of majority class samples
- Synthetic data generation: Create artificial samples to balance the dataset
| Technique | Pros | Cons |
|---|---|---|
| Oversampling | Preserves all data | Risk of overfitting |
| Undersampling | Reduces training time | Potential loss of information |
| Synthetic data | Maintains original distribution | May introduce artificial patterns |
B. Handling extreme values and outliers
Extreme values and outliers can significantly impact skewness and kurtosis. Address these issues using:
- Winsorization: Cap extreme values at a specified percentile
- Trimming: Remove a small percentage of extreme values
- Imputation: Replace outliers with more representative values
C. Data transformation techniques
Transform your data to reduce skewness and kurtosis:
- Log transformation: Effective for right-skewed data
- Square root transformation: Useful for moderately skewed data
- Box-Cox transformation: Versatile method for various distributions
- Yeo-Johnson transformation: Handles both positive and negative values
By applying these techniques, you can significantly improve the quality of your dataset, making it more suitable for various analytical and machine learning tasks. In the next section, we’ll examine real-world case studies that demonstrate the impact of addressing skewness and kurtosis in data analysis projects.
Take the help of www.editverse.com to audit and improve your statistics!
Now that we’ve explored the intricacies of skewness and kurtosis in data analysis, it’s time to elevate your statistical game. www.editverse.com offers a powerful suite of tools to audit and enhance your statistical analyses, ensuring that your insights are both accurate and impactful.
Key Features of www.editverse.com
- Automated Skewness and Kurtosis Detection: Quickly identify asymmetry and peakedness in your data distributions.
- Interactive Data Visualization: Gain deeper insights through dynamic graphical representations of your statistical measures.
- Comprehensive Outlier Analysis: Detect and address outliers that may skew your results.
- Advanced Preprocessing Techniques: Apply sophisticated methods to normalize your data and improve statistical validity.
How www.editverse.com Can Improve Your Analysis
- Streamlined Workflow
- Enhanced Accuracy
- Time-saving Automation
- Expert Guidance
Comparison of www.editverse.com with Traditional Methods
| Feature | www.editverse.com | Traditional Methods |
|---|---|---|
| Speed | Rapid analysis | Time-consuming |
| Accuracy | High precision | Prone to human error |
| Visualization | Interactive charts | Static graphs |
| Preprocessing | Automated options | Manual adjustments |
| Expertise Required | Minimal | Extensive |
By leveraging the advanced capabilities of www.editverse.com, you can transform your approach to data distribution analysis and descriptive statistics. This powerful platform not only simplifies complex statistical processes but also provides you with the tools to make more informed decisions based on your data’s shape and characteristics.

Skewness and kurtosis are powerful tools in the data analyst’s arsenal, providing critical insights into the shape and characteristics of data distributions. By understanding these measures, analysts can make more informed decisions about data preprocessing, modeling, and interpretation. Skewness reveals asymmetry in data, while kurtosis offers information about the presence of outliers and the overall shape of the distribution.
As we’ve explored, there are numerous practical applications for skewness and kurtosis across various industries. From finance to environmental science, these measures help identify potential risks, anomalies, and patterns in data. By leveraging the right tools and techniques, data professionals can effectively analyze and address skewness and kurtosis in their datasets, leading to more accurate and reliable analytical outcomes. Remember, proper handling of these distribution characteristics during data preprocessing is crucial for developing robust and trustworthy models.